Loot is an integral feature of many games. A change in kit, a powerful addition to your loadout, or a shiny new fanged hat can add variety to the core gameplay loop and provide short and long term goals for players to achieve. But how is it done? This article will explain the simple algorithm behind loot distribution, exploring its underpinnings in statistics as an application of the cumulative distribution function on a discrete set of elements.
Video
Motivation
This design pertains to random loot acquisition by the player, with common use cases including the distribution of loot on the ground in a Battle Royale or the presentation of treasure rooms in a dungeon crawler. Let’s say that the player initiates an event resulting in the acquisition of some piece of loot with a rarity R, drawn from a loot pool containing all possible loot items.
In most cases, it doesn’t make sense to assign individual probabilities to each piece of loot, as readjustment would become a nightmarish task, and picking through potentially thousands of unique items to assign each a probability is an immensely tedious and unnecessary task.

Fig. 1: An example of individual probability assignment, where each item is given an individual (but not necessarily unique) probability of being drawn
Tiers
This problem is usually resolved by creating tiers, essentially batching items into groups of rarity, with equal probabilities among the group. For a “rare” group with 12 items and a 24% chance of being selected, each rare item would individually have a 2% chance of being selected from the batch.

Fig. 2: An Example of Loot tiers.
It follows then, that a tier is selected randomly based on its weight, and in that tier each item has an equal chance of being obtained. An item is randomly selected from that tier for the player. This is the basic mechanism of a tiered loot distribution, creating groups of items with a discrete probability distribution.
Representing Weights
Two models of representing weights exist - the absolute and relative modes.
The absolute probability mode presents probabilities relative to the whole - that is, tier weights are normalized and must add up to unity, or 100%. It is clearly better for showing the probability of obtaining items of each tier against the whole, but would be difficult to adjust, as adding or removing tiers would necessarily disrupt the sum, and the change of a single probability necessitates the alteration of at least one other.
The relative probability mode presents probabilities relative to a base of 1, and are essentially unnormalized. The easiest way to do this is to set the item of the highest rarity to have a relative weight of 1, and the addition of other tiers with higher relative weights. If the common tier had a weight of five, it would be five times more likely to appear than the rare base tier. This makes it easier to adjust, as the change of relative weights wouldn’t necessarily break the system, and it becomes much easier to set weights, as it’s generally more natural in my experience to consider weights in proportion to one another than against the whole.
Implementation
Though this seems a simple system to implement, it’s not really obvious how to create a weighted probability. Most programming languages support some ability to access random numbers, but it’s unusual to see one that supports weighted selection. My code is presented in C#, as I wrote this for my Unity-based game, but its meaning should be clear enough as I don’t use any C# specific syntax/notation. One thing to note, however, is that Unity’s Random.Range(x,y) function returns a number in the range [x,y).
Naively, one might generate a normalized random number (a float between 0 and 1, inclusive) and check if it’s less than a weight - this is a bad idea, and requires one to manually compute a cumulative sum.
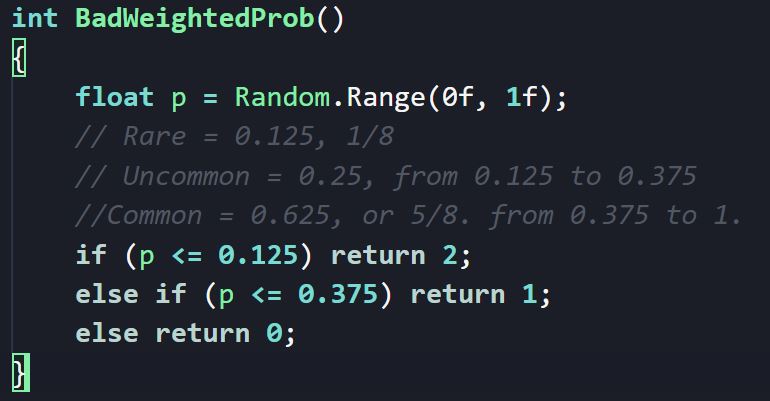
A better method would be to implement a running total, passing in a series of tiers (encoded as enumerations, integers, strings or other objects) and weights (encoded as numeric values). Then, one would first sum up the tiers to compute the total weight by iterating through the list of weights.
A random number is then generated between zero and the sum of the weights, and then the main loop of the function begins: One can iterate through the tiers, and in each step add the weight of a tier to the running total. If that running total, at any point, exceeds the random number, the loop is stopped and the corresponding tier that was just added to the total is returned.
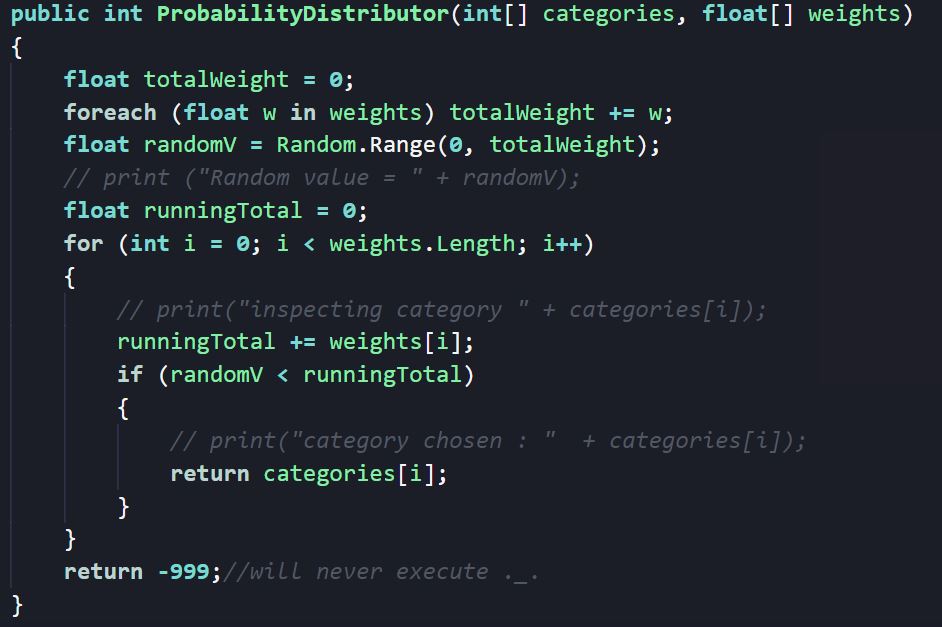
Visually, this method involves generating a line segmented into discrete chunks of varying size, and dropping a marker randomly on the line. The program moves from the start of one tier to the end, and checks if it has passed the marker’s position with a simple less than or equals test. If it has, the tier has been located. If it hasn’t, the program continues to the next tier. Notice that with this method, the order of the tiers/weights is arbitrary and doesn’t affect the execution of the code.
 Fig. 3: A line marked with varying discrete weights. A marker can be dropped, and one can advance from one tier to the next in discrete steps, checking after each tier change if it has passed the marker.
Fig. 3: A line marked with varying discrete weights. A marker can be dropped, and one can advance from one tier to the next in discrete steps, checking after each tier change if it has passed the marker.
Conclusion
The design of a loot distribution system is really quite simple, and suggests an near-ubiquitous use of weighted probabilities in game design. Extensions to this system exist, like the creation of dependent probabilities, where, if the player can attain multiple loot items, the probability of getting each one isn’t random, but biased depending on the other items. For example, an enterprising microtransaction engineer might reduce the probability of getting a further rare and valuable player skin in consecutive rolls after one is already obtained. While being ethically questionable, it suggests there is utility to dependent probability systems, not only the independent system I have described in this post.
Additionally, if you liked the motion graphics in my video, check out my series: The Elements of Motion Graphics! It goes over how to create complex motion graphics for free in Blender by building on the fundamentals, and it’s completely free to watch on Youtube, or to read on my website. Thank you for reading and enjoying my content, and I hope you find it useful!
